Introduction

Les termes de fonction de coût, fonction de perte et de fonction objectif sont très utilisés dans de multiples domaines et sont tous étroitement liés. Dans cet article on se concentre plus sur les usages adaptés au machine learning.

Fonction de coût

On considère un ensemble de test avec M comme le nombre d’occurrences et une fonction de coût \(J\) avec \(\theta_{0},\theta_{1}\) comme paramètres et une fonction hypothèse de format \(h_{\theta}(x)=\theta_{0}+\theta_{1}x\). On considère aussi dans un contexte de machine learning, \(x^{(i)}\) représentant les “variables d’entrée” et \(y^{(i)}\) les “sorties” de la fonction. On peut alors considérer : \[\begin{aligned}
J(\theta_{0},\theta_{1})=\frac{1}{2M} \sum_{i=1}^{M} (h_{\theta}(x^{(i)})-y^{(i)})^2\end{aligned}\]

On nomme aussi cette approche la “Méthode des moindre carrés”.¹ On note \(X\) l’espace des valeurs d’entrée et \(Y\) l’espace des valeurs de sorties avec \(X = Y = \mathbb{R}\).
Pour décrire un problème de Machine Learning supervisé, de manière formelle, on considère que, étant donné un jeu de test, pour “apprendre”, la fonction \(h : X \rightarrow Y\) de telle manière que \(h(x)\) permet une bonne prédiction des valeurs \(y\). Pour des raisons historiques dans le domaine du Machine Learning, on appelle hypothèse la fonction \(h\) (même si ce terme n’est pas parfaitement adapté). Dans le cas d’une progression linéraire, la fonction de coût va permettre de déterminer la meilleure approximation linéaire des données disponibles.

La fonction hypothèse s’écrit : \(h_{\theta}(x)=\theta_{0}+\theta_{1}x\) avec \(\theta_{i}\) appelés paramètres. Il s’agira de choisir \(\theta_{0},\theta_{1}\) de telle manière que \(h_{\theta}(x)\) est proche de \(y\) dans nos jeux de données \((x,y)\).

En synthèse cela revient à Minimiser avec \(\theta_{0},\theta_{1}\) et donc de minimiser la différence des carrés entre la sortie de l’hypothèse et la valeur réelle \((h_{\theta}(x)-y )^2\).

On a donc respectivement : \[\label{eq1}
\textbf{Minimiser} \ \theta_{0},\theta_{1} \quad \frac{1}{2M} \sum_{i=1}^{M}(h_{\theta}(x^{(i)})-y^{(i)})^2\]

\[\label{eq2}
h_{\theta}(x^{(i)})=\theta_{0}+\theta_{i}x^{(i)}\]

\[\label{eq3}
J(\theta_{0},\theta_{1})=\frac{1}{2M} \sum_{i=1}^{M} (h_{\theta}(x^{(i)})-y^{(i)})^2\]

Progression linéaire : exemple et simplifications

On considère un jeu de données simplifié (croix noires) : \((1,1) (2,2) (3,3)\) et les représentations graphiques \(\theta_{1}=1\) (ligne bleue) et \(\theta_{1}=0.5\) (ligne verte) :

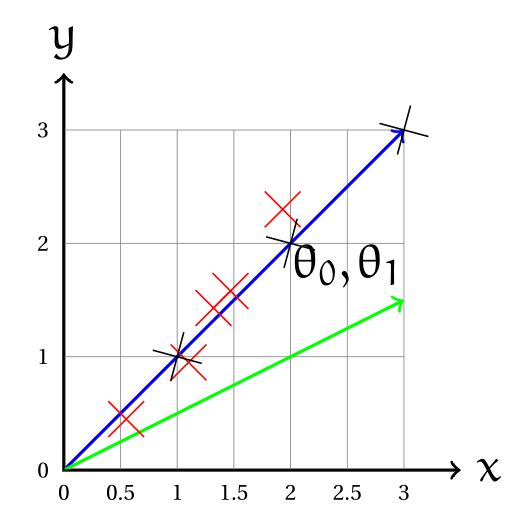
Hypothèse 1 : \(h_{\theta}(x)=\theta_{0}+\theta_{1}x\)

Paramètres : \(\theta_{0},\theta_{1}\)
Fonction de coût : \(J(\theta_{0},\theta_{1})=\frac{1}{2m} \sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})^2\)
Objectif : minimiser \(\theta_{0},\theta_{1} \ J(\theta_{0},\theta_{1})\)

Hypothèse 2 : \(h_{\theta}(x)=\theta_{1}x\)

Paramètres : \(\theta_{1}\)
Fonction de coût : \(J(\theta_{1})=\frac{1}{2m} \sum_{i=1}^{M}(h_{\theta}(x^{(i)})-y^{(i)})^2\)
Objectif : minimiser \(\theta_{1} \ J(\theta_{1})\)

Pour \(\theta_{1}=1,\ J(\theta_{1})=\frac{1}{2m}(0^2+0^2+0^2)\) so \(J(1)=0\)
Pour \(\theta_{1}=0.5\), et le jeu de données \((1,1) (2,2) (3,3)\), on a :

\[\label{eq4}
\begin{aligned}
J(0.5) & = \frac{1}{2m} \sum_{i=1}^{m} (h_{1}(x^{(i)})-y^{(i)})^2 \\
& = \frac{1}{2*3} \sum_{i=1}^{3} (h_{1}(x^{(i)})-y^{(i)})^2 \\
& = \frac{1}{6} [(h_{1}(x^{(1)})-y^{(1)})^2 + (h_{1}(x^{(2)})-y^{(2)})^2 + (h_{1}(x^{(3)})-y^{(3)})^2 )] \\
& = \frac{1}{6} [(0.5-1)^2 + (2-1)^2 + (1.5-3)^2 )] \\
& = \frac{1}{6} [(-0.5)^2 + (1)^2 + (-1.5)^2 )] \\
& = \frac{1}{6} [0.25 + 1 + 2.25 ] \\
& = \frac{3.5}{6} \\
& \approx 0.583
\end{aligned}\]

Revue des termes

D’un point de vue sémantique les termes fonction de perte et fonction de coût sont plus ou moins synonymes et il n’existe pas de convention parfaite de distinction. La fonction de perte (loss function²) est généralement une fonction définie sur un point de données, une prédiction et une étiquette, et mesure la pénalité.³ Des exemples sont :⁴

square loss \(l(f(x_i|\theta),y_i) = \left (f(x_i|\theta)-y_i \right )^2\), utilisé en régression linéaire,⁵
hinge loss⁶ \(l(f(x_i|\theta), y_i) = \max(0, 1-f(x_i|\theta)y_i)\) utilisé en SVM (Support Vector Machine⁷)

Une fonction de coût est souvent un terme plus général. Il peut par exemple être composé de sommes de fonctions de pertes et des régularisations. Par exemple :

Méthode des moindres carrés (Mean Squared Error) \(MSE(\theta) = \frac{1}{N} \sum_{i=1}^N \left (f(x_i|\theta)-y_i \right )^2\)
SVM cost function \(SVM(\theta) = \|\theta\|^2 + C \sum_{i=1}^N \xi_i\) (prononcer xi pour \(\xi\))(comporte des contraintes additionnelles : \(\xi\), C, training set…etc )