Contrôles d’accès basés sur treillis et modèles de sécurité

Franck Jeannot, U638, Montréal, Canada, Décembre 2019 : v1.0 ; Dernière version : Janvier 2021 : v1.2

1. Treillis et sécurité

Les contrôles d’accès basés sur treillis ou LBAC sont utilisés pour définir des niveaux de sécurité des objets et des sujets via des labels ou étiquettes de sécurité en renforçant un flux d’information unidirectionnel². Quand un label est sur un objet, on parle de classification de sécurité, alors que si le label est sur un sujet, on parle d’habilitation de sécurité (security clearance). Les étiquettes de sécurité forment un treillis tel que l’élément le plus haut du treillis est le plus sensible³.

Les contrôles LBAC peuvent être utilisés pour la confidentialité, l’intégrité, ces 2 composantes ou bien des aggrégations diverses de polices comme le modèle « Muraille de chine ». Le modèle de Bell-LaPadula (confidentialité) [4] [5] décrit un jeu de règles qui proscrit tout flux d’information d’un haut niveau vers un plus bas niveau. Une appellation LaBAC Label-Based Access Control [6] existe aussi mais n’est pas développée ici.

Les LBAC sont essentiellement des Contrôles d’Accès Obligatoires ou MAC (Mandatory Access Controls) qui sont typiquement ajoutés en plus ⁴ de classiques contrôles d’accès discrétionnaires DAC. Dans le domaine des contrôles d’accès de sécurité, on aura alors :

• • des niveaux de sécurité H avec des classifications linéaires ≤

• • des catégories C tels que les noms de projet, divisions de l’entreprise, etc.

• • des étiquettes de sécurité qui sont des paires (h,c) où h ∈ H et c ⊆ C

On définit une étiquette de sécurité par la paire (niveau de sécurité H, ensemble de catégories C).

2. Treillis et définitions

On retrouve diverses définitions dans la littérature, il en est repris plus bas des éléments importants. Les treillis ont des connexions avec la théorie des graphes [8].

Définition simplifiée. On appelle treillis un ensemble non vide et partiellement ordonné (4) dans lequel toute partie finie admet une borne inférieure et une borne supérieure ⁵ . Un poset (de l’anglais partially ordered set, en français “ensemble partiellement ordonné”) formalise la notion intuitive d’ordre ou d’arrangement entre les éléments d’un ensemble. Un poset est un ensemble muni d’une relation d’ordre qui indique que pour certains couples d’éléments, l’un est plus petit que l’autre ⁶ .

2.1. Diagramme saggittal et Diagramme de Hasse

Un diagramme saggital sert à représenter une relation d’un ensemble fini vers un ensemble fini dans lequel chaque couple est représenté par une flèche. Un diagramme de Hasse ⁷ , est une représentation visuelle d’un ordre fini, c’est une version simplifiée ⁸ d’un diagramme saggital ^{9 10} et souvent utilisé pour représenter les treillis.

2.2. Opérateurs binaires Join ∨ et meet ∧

En mathématiques, spécifiquement dans la théorie des ordres, les notions d’opérateurs join et meet [8] d’un sous-ensemble S d’un ordre partiel P sont respectivement les supremum de S , noté ∨S et l’infimum de S noté ∧S. Selon le mathématicien Gian-Carlo Rota [13] : « Lattices are partially ordered sets in which least upper bounds and greatest lower bounds of any two elements exist. Dedekind [14] discovered that this property may be axiomatized by identities. A lattice is a set on which two operations are defined, called join and meet and denoted by ∨ and ∧ which satisfy the idempotent, commutative and associative laws, as well as the absorption laws : »

a∨(b∧a) = a
a∧(b∨a) = a

Exemple plus bas d’un diagramme de Hasse qui décrit un poset a 4 éléments : a,b, le join de a et b (a∨b) ou supremum ou least upper bound et le meet de a et b (a∧b) ou infimum ou great lower bound ¹¹ . Ici chaque paire dans ce poset à a la fois un meet et un join et donc peut être classée comme un treillis.

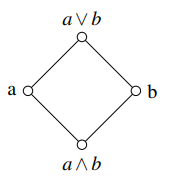
Définition algébrique. [16] Un ensemble ordonné L est appelé un treillis si deux opérations binaires, meet et join, qui assignent à toute paire a,b des éléments de L, un élément unique a∧b (meet de a et b) et un élément a∨b (join de a et b) de telle manière que les axiomes suvants du treillis soient satisfait. On définit a,b et c ∈ L. Alors :

L1 : (a∧b)∧c = a∧(b∧c),      L2 : (a∨b)∨c = a∨(b∨c)
L3 : a∧b = b∧a,       L4 : a∨b = b∨a
L5 : a∧(a∨b) = a        L6 : a∨(a∧b) = a

L1-L2 : loi associative (associative law) ; L3-L4 : loi commutative (commutative law) ; L5-L6 : loi d’absorption (absorption law) ¹²

Si L est un treillis, alors a∧a = a et a∨a = a pour tous les a de L.

3. Treillis et origines

Les notions de treillis ont été d’abord introduites par George Boole (1824) puis Ernst Schröder en 1890 [16] [18]. Après cela, les travaux de P.G. Dirichlet (1894) [19] [20], ont été réutilisé en 1897, par Richard Dedekind qui fut crédité de la découverte des treillis distributifs et modulaires. En 1920, le mathématicien Norvégien Thoralf Albert Skolem apporta des éléments sur la théorie des treillis (Gruppenkalkul) [21]. Sur ces bases, dans les années 1930, Garrett Birkhoff fit de larges contributions à ce qui fut finalement qualifiée alors comme la Théorie des treillis [22] [23] [24]. Dans les années 1970, Bell, Biba, LaPadula, Denning [25] ont avancé la recherche dans le domaine des LBAC. Par la suite, nombre de ces modèles ont été implémentés, essentiellement en applications militaires. Par la suite Sandhu [26] en 1993 a complété la formalisation des LBAC. Bien que la théorie des treillis ait traversé différentes étapes de développement avec des approches et des attentes changeantes, ce domaine a considérablement augmenté chaque décennie depuis sa naissance [13] [27].

4. Ensembles totalement et partiellement ordonnés

4.1. Hiérarchie et précédence

Si on considère un ensemble P : avoir une hiérarchie sur P permet de définir une relation de précédence sur P : p est une relation avec q si p précède q dans la hiérarchie [10].

4.2. Propriétés de la précédence

• antisymétrique : si p et q sont différents et si p précède q alors q ne peut pas précéder p

• transitive : si p précède q et p précède r alors p précède r

• réflexive : p ≤ p

4.3. Ordre

Une relation réflexive, antisymétrique et transitive s’appelle une relation d’ordre. Un ensemble muni d’une relation d’ordre est un ensemble ordonné.

Autre Formalisation.
Une relation R sur un ensemble A est appelée ordre partiel si elle est réflexive, anti-symétrique et transitive. Un ensemble A avec une relation d’ordre partiel R est appelé un ensemble partiellement ordonné ou poset. Ce poset est noté (S,R) ¹³ .

• Les relations ≤ et ≥ sur ℕ sont des relations d’ordre

• Les relations < et > sur sur ℕ n’en sont pas

• sur ℕ^∗, la relation a divise b, notée a|b est une relation d’ordre (a divise b s’il existe k ∈ℕ^∗ tel que b = ka ). Par exemple, 3|24.

• Relations d’ordre fréquentes : ≤,≥,≼,≽,⊑,⊒,⊆,⊇,| etc. Une notation générale est : ≪ et ≫.

4.4. Vocabulaire conventionnel d’une relation d’ordre

Si x ≪ y, on dit que x est un minorant de y (x minore y) et y est un majorant de x (y majore x).

4.5. Poset

La notion d’« ensemble partiellement ordonné », de l’anglais poset [29], partially ordered set a été utilisée par Birkhoff dans son livre Lattice theory (1940) [22] [30]. C’est un ensemble muni d’une relation d’ordre ¹⁴ . Un poset (P,≤) est un ensemble P avec une relation ≤, appelée ordre partiel, tel que ¹⁵ :

• Pour tous les p ∈ P , on a p ≤ p (réflexivité)

• Pour tous les p,q ∈ P , si p ≤ q et q ≤ p alors p = q (antisymétrie)

• Pour tous les p,q,r ∈ P , si p ≤ q et q ≤ r alors p ≤ r (transitivité)

On dit que p et q sont comparables si p < q ou p > q, et ils sont incomparables autrement. On dit que q couvre p si q > p et qu’il n’y a pas de r ∈ P tel que q > r > p. Quand q couvre p, on
écrit q⋗p. Pour pointer le fait qu’un ordre n’est pas total on dit qu’il s’agit d’un ordre partiel : certains éléments sont incomparables dans un tel ordre. Un ensemble totalement ordonné est un
ensemble muni d’une relation d’ordre total. Poset : autre formulation. [20] Un poset est un système 𝒫 = (P,≤) où P est non vide et ≤ est une relation binairesur P satisfaisant pour tous les x,y,z ∈ P :

Par définition un treillis est un poset, cependant un poset n’est pas nécessairement un treillis.

5. Polices de flux d’informations

Les stratégies de flux d’informations concernent le flux des informations d’une classe de sécurité à une autre. Dans un système, les informations circulent réellement d’un objet à
un autre. Des exemples typiques d’objets sont les fichiers et les répertoires d’un système d’exploitation, ainsi que les relations et les nuplets dans un système de base de données [26].

5.1. Diagramme de Hasse avec 3 catégories

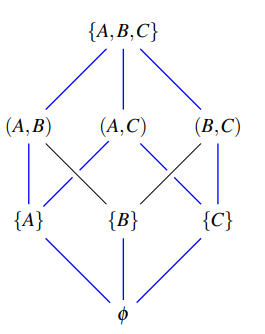
Le modèle de contrôle d’accès basé sur treillis plus bas (fig. 2) est un exemple de Diagramme de Hasse, selon (Ravi S. Sandhu, 1993) [26] qui montre un treillis d’une police avec
3 catégories A,B,C et qui peuvent dénoter des catégories comme “salaire”, “medical” et “education”. Au plus haut niveau d’accès on trouve la boîte A,B,C. Un sujet à
ce niveau, a accès à tous les objets du treillis (voir aussi p. 81 de (Eric Conrad, 2011) [31]). Dans le second tiers du treillis, on observe que chaque objet a une limite
distincte haute et basse. Par exemple si un sujet a accès à l’objet A,C, les seuls objets visibles dans le treillis sont les objets A et C, qui sont ses deux GLB (Greatest
Lower Bound). Dans ce cas, le sujet ne pourrait avoir par exemple visibilité sur l’objet B.

5.2. Exemple d’accès à des ensembles de données

Dans (Meadows, 1990) (p. 3 de [32]) est donné un exemple de base de données qui se compose de six ensembles : A, B, C, D, E et F.

A, B, D et F ne sont pas classés (U=Unclassified), tandis que C et E sont (S) Secrets. Les agrégats exceptés sont B, D, qui est étiqueté Secret. Enfin A, B, C et C, E, qui sont (TS) Top Secret :

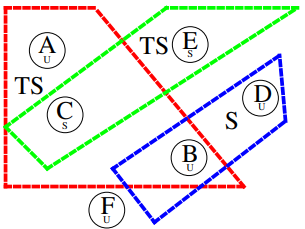
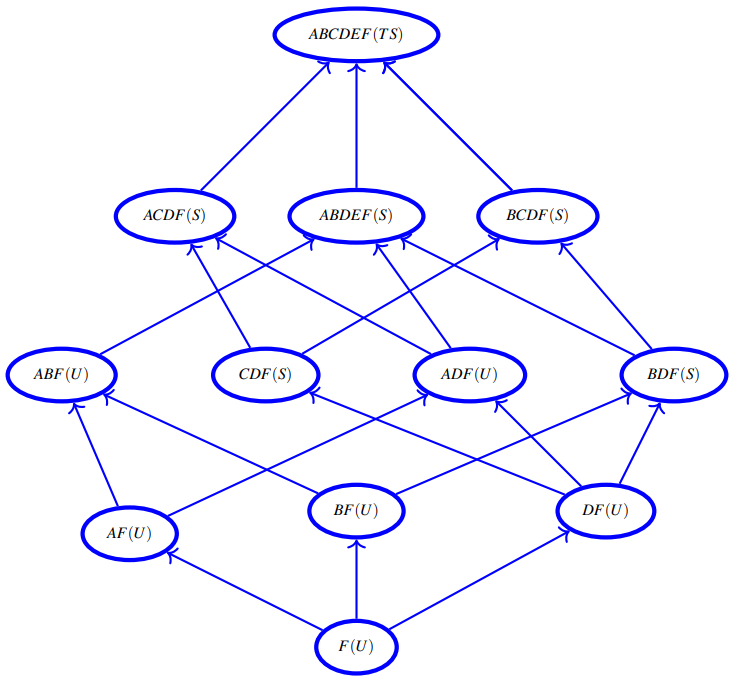
Au final un modèle d’accès basé sur treillis est construit (ref p. 6 de [32])) :

Références

1. CISSP Study guide, p. 324, Stewart (2015), [1]↩︎
2. Sandhu (1998), p. 35/50 de [2]↩︎
3. Sabri (2009), p. 5 de [3]↩︎
4. Sandhu (1994), [7]↩︎
5. Wikipedia [9]↩︎
6. http://dictionnaire.sensagent.leparisien.fr/Poset/fr-fr/↩︎
7. Du mathématicien allemand Helmut Hasse↩︎
8. Voir Labourel p7/68 [10]↩︎
9. Voir pp 17-18 de [11]↩︎
10. Le mot « sagittal » vient du mot latin sagitta qui veut dire « flèche », [12]↩︎
11. p. 33 de [15]↩︎
12. Paragraphe 14.8 LATTICES, page 346 de [17]↩︎
13. Trad. libre de [28]↩︎
14. relation binaire dans cet ensemble qui permet de comparer ses éléments entre eux de manière cohérente↩︎
15. on parle des 3 axiomes de réflexivité, anti-symétrie, transitivité↩︎